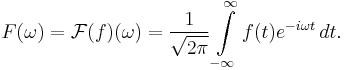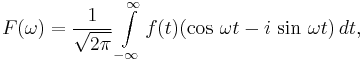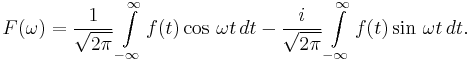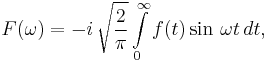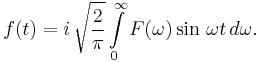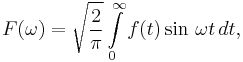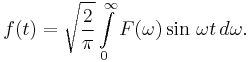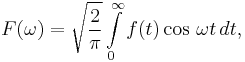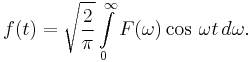Sine and cosine transforms

In mathematics, the Fourier sine and cosine transforms are special cases of the continuous Fourier transform, arising naturally when attempting to transform odd and even functions, respectively.

The general Fourier transform is defined as:

F(\omega) = \mathcal{F}(f)(\omega) = \frac{1}{\sqrt{2\pi}} \int\limits_{-\infty}^\infty f(t) e^{-i\omega t}\,dt.

Expanding the integrand by means of Euler's formula results in:

F(\omega)=\frac{1}{\sqrt{2\pi}} \int\limits_{-\infty}^\infty f(t)(\cos\,{\omega t} - i\,\sin{ \,\omega t})\,dt,

which may be written as the sum of two integrals:

F(\omega)=\frac{1}{\sqrt{2\pi}} \int\limits_{-\infty}^\infty f(t)\cos\,{\omega t} \,dt - \frac{i}{\sqrt{2\pi}} \int\limits_{-\infty}^\infty f(t)\sin\,{\omega t}\,dt.

The Fourier sine transform and Fourier cosine transform are derived from this.

Contents

Fourier sine transform

The Fourier sine transform is a special case of the continuous Fourier transform, arising naturally when attempting to transform an odd function. From the general Fourier transform noted above, if f(t) is assumed to be an odd function, the product f(t)cosωt is also odd whilst the product f(t)sinωt is an even function. Since the integral is being computed over an interval symmetric about the origin (i.e. -∞ to +∞), the first integral must vanish to zero, and the second may be simplified to give:

F(\omega)= -i\,\sqrt{\frac{2}{\pi}} \int\limits_{0}^\infty f(t)\sin\,{\omega t} \,dt,

which is the Fourier sine transform for odd f(t). It is clear that the transformed function F(ω) is also an odd function, and a similar analysis of the general Inverse Fourier transform yields a second sine transform, namely:

f(t)= i\,\sqrt{\frac{2}{\pi}} \int\limits_{0}^\infty F(\omega)\sin\,{\omega t} \,d\omega.

The numerical factors in the transforms are defined uniquely only by their product, as discussed for general continuous Fourier transforms. For this reason the imaginary units i and -i can be omitted, with the more commonly seen forms of the Fourier sine transforms being:

F(\omega)= \sqrt{\frac{2}{\pi}} \int\limits_{0}^\infty f(t)\sin\,{\omega t} \,dt,

and

f(t)= \sqrt{\frac{2}{\pi}} \int\limits_{0}^\infty F(\omega)\sin\,{\omega t} \,d\omega.

Fourier cosine transform

The Fourier cosine transform is a special case of the continuous Fourier transform, arising naturally when attempting to transform an even function. From the general Fourier transform noted above, if f(t) is assumed to be an even function, the product f(t)cosωt is also even whilst the product f(t)sinωt is an odd function. Since the integral is being computed over an interval symmetric about the origin (i.e. -∞ to +∞), the second integral must vanish to zero, and the first may be simplified to give:

F(\omega)= \sqrt{\frac{2}{\pi}} \int\limits_{0}^\infty f(t)\cos\,{\omega t} \,dt,

which is the Fourier cosine transform for even f(t). It is clear that the transformed function F(ω) is also an even function, and a similar analysis of the general inverse Fourier transform yields a second cosine transform, namely:

f(t)= \sqrt{\frac{2}{\pi}} \int\limits_{0}^\infty F(\omega)\cos\,{\omega t} \,d\omega.

The numerical factors in the transforms are defined uniquely only by their product, as discussed for general continuous Fourier transforms.

See also

References